 |
 |
|
||||||||||||||||
*第42回 N値計算法の中の『L』の原理となった柱カウンターウェイト検証実験 後編1 |
||||||||||||||||
*第43回 N値計算法の中の『L』の原理となった柱カウンターウェイト検証実験 後編2 |
||||||||||||||||
*第44回 N値計算法の中の『L』の原理となった柱カウンターウェイト検証実験 後編3 |
||||||||||||||||
*第45回 N値計算法の中の『L』の原理となった柱カウンターウェイト検証実験 後編4 |
||||||||||||||||
*第46回 N値計算法の中の『L』の原理となった柱カウンターウェイト検証実験 後編5 |
||||||||||||||||
|
*第47回 N値計算法の中の『L』の原理となった柱カウンターウェイト検証実験 後編6
|
||||||||||||||||
|
*第48回 N値計算法の中の『L』の原理となった柱カウンターウェイト検証実験 後編7 |
||||||||||||||||
| 4.考察 | ||||||||||||||||
| 4−1. 実験結果全体の考察 | ||||||||||||||||
| (1)押さえ込み効果(カウンターウェイト)の検証 | ||||||||||||||||
| 水平力による耐力壁の剛体的回転により、柱が浮き上がった際、長期軸力よりもかなり大きな押さえ込み効果すなわちカウンターウェイトが存在することが確認できた(次節参照)。 |
||||||||||||||||
| また、柱の浮き上がりが大きくなるほど、カウンターウェイトが増大し、それに伴って水平耐力も増大することが確認できた。No.4-1はNo.3-3に、耐力壁数・位置は変えずにL字形に増築したものであるが、カウンターウェイトが増大し(約1470(kg)の増加)、その結果700(kg)近くの試験体全体の水平耐力の増加が見られた。これは、継ぎ手のメス側がオス側増築部分の梁を持ち上げ、浮き上がり範囲が増えたことが原因であると思われる。 | ||||||||||||||||
| (2)梁継ぎ手のメス・オスの方向とカウンターウェイトの関係 | ||||||||||||||||
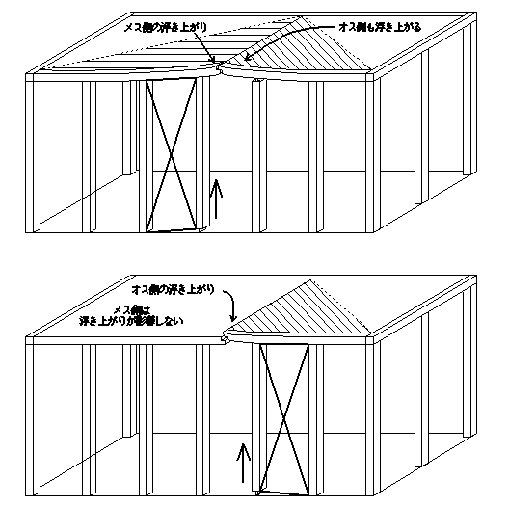
| 梁継手のメス側が浮き上がった場合は、同時にオス側も持ち上げられる形となった。今回の継ぎ手は、はめ込んだだけの形で、金物等で緊結されていないので、オス側が持ちあがった場合、オス側のみが持ち上がる現象が見られた(これは、金物がついていても、短冊金物程度の緊結力のものでも、同様の現象が予想される)。 | ||||||||||||||||
| もし、オス側が浮いた場合もメス側を持ち上げるような、継手の金物などの緊結がなされていれば、カウンターウェイト増大につながり、耐力の増大につながるであろう。 | ||||||||||||||||
 |
||||||||||||||||
| 図86 | ||||||||||||||||
| (3)耐力壁による水平力から柱突き上げ力への変換効率 | ||||||||||||||||
全体的に1.7〜2.6程度の間にあり、耐力壁の縦横比率による2.90と比べると、約60〜90%程度の値であった(参照:後編6の表6)。 |
||||||||||||||||
| 80〜90%程度のものは耐力壁以外の要素による抵抗が多少存在していることが考えられるが、60%とかなり低めの値のものは、ロードセル値の計測値が低めにでている(特に斜体で示した推定値のもの)など、ロードセル計測不良の原因も考えられる(P33〜P35の図20〜22のグラフできれいな山形を描いていないものや、最大変位1/30rad時にピークになっていないものなど)。 | ||||||||||||||||
| (4)梁及び根太等の方向のカウンターウェイトへの影響 | ||||||||||||||||
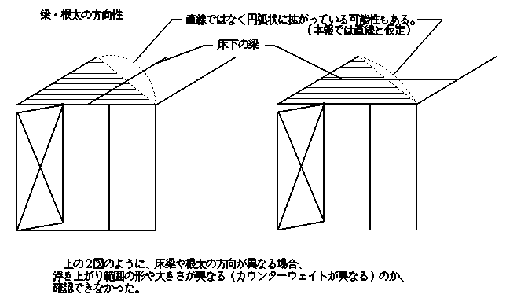
| 今回の試験結果を見る限りでは、根太及び梁の架かりかたの違いは、確認できなかった(下図参照)。 床下や、2次梁の浮き上がりの計測も行うべきであった。 ただし、カウンターウェイトを、複数の突き上げ柱に分割する場合、長期軸力を計算するときと同様に、梁や根太の方向に注意して計算する必要がある。 |
||||||||||||||||
 |
||||||||||||||||
| 図87 | ||||||||||||||||
| (5)直交耐力壁の有無によるカウンターウェイトへの影響について | ||||||||||||||||
| 直交耐力壁の有無による影響はほとんど見られなかった。 今回の試験体の合板耐力壁は梁に直接釘打ちされておらず(載荷方向の耐力壁は土台とも釘打ちされていない)、また、変位制御での実験であるため建物のねじれも発生しないので、カウンターウェイト・水平耐力に直交耐力壁の影響はほとんどなかったといえる。 ただし、直交壁(または耐力壁)の柱頭柱脚が金物で緊結されている場合(No.3-2、3-4、4-4)、金物による押さえ込みが追加され、金物なしに比べ耐力の上昇が見られた((6)参照)。 |
||||||||||||||||
| (6)直交壁構面柱頭部の金物の影響 | ||||||||||||||||
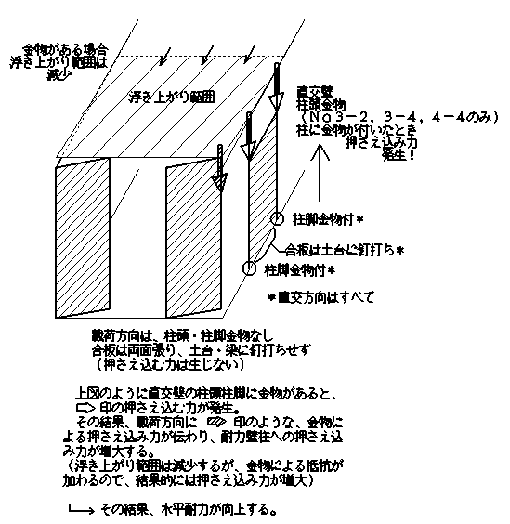
| 直交壁構面の柱頭部(Y通り(直交方向)のみ柱脚部はすべて金物で緊結し、合板も土台に釘打ちされている)に金物が設置されている場合、若干(1割程度)浮き上がり範囲(カウンターウェイト)が減少するが、金物抵抗がある分水平耐力が上昇した。 カウンターウェイトは減ったものの、直交壁柱頭の金物があることにより、その直交梁による押さえ込み抵抗がそれ以上に増大した結果である。 |
||||||||||||||||
 |
||||||||||||||||
| 図88 | ||||||||||||||||
| 4−2. 柱カウンターウェイトと水平耐力 | ||||||||||||||||
| 4−2−1 柱カウンターウェイトについて | ||||||||||||||||
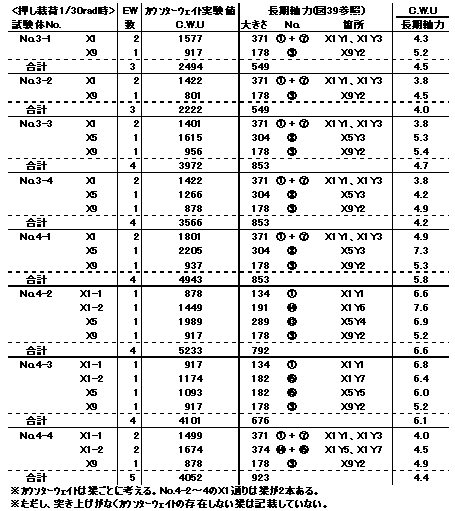
| 柱カウンターウェイトは、耐力壁の剛体的回転により梁が浮き上がった際の、柱の長期軸力以上の上階からの押さえ込み効果をいう。 本実験の結果では、終局耐力時(層間変形角1/30rad時)に長期軸力の4〜7倍程度の押さえ込み効果があることが確認できた(下表参照)。 しかし、梁の架かり方や柱の位置によって、柱の長期軸力は異なり、長期軸力が非常に大きい場合は、カウンターウェイトと長期軸力にほとんど差がない場合もあると思われる。 また、壁が土壁などの剛体的回転が生じないようなものの場合では、浮き上がりが少ないのでカウンターウェイトは小さく、長期軸力とほとんど差がなくなるものと思われる。 |
||||||||||||||||
 |
||||||||||||||||
| 表8 | ||||||||||||||||
| また、カウンターウェイトの大きさは梁単位で、その梁上部の壁、その梁にとりつく梁(2次梁)や床から伝わる押さえ込みを考える。梁の浮き上がりにより、それに連れ2次梁や床がどこまで浮き上がるかが、カウンターウェイトの大小に影響する。 本実験では、大きさの推定できないジャッキの押さえ込み効果や、ロードセルの接触不良など、柱頭の軸圧縮力による荷重値の信憑性が小さいと考えられるため(参考程度にした)、浮き上がりの計測値から、その範囲を推測し、カウンターウェイトを求めた。 また、今回の実験では引き載荷時については、柱ロードセル計測値が正しく計測されていなかったり、載荷部ジャッキ部抵抗の影響大きく受けていたりしていたことから、参考程度とし、押し載荷時の実験データを中心にカウンターウェイトの考察を行った。 |
||||||||||||||||
| 4−2−2 変換効率と水平耐力 | ||||||||||||||||
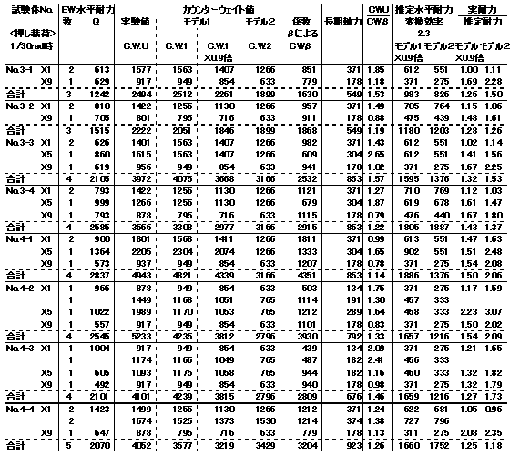
| 水平荷重と、耐力壁の剛体的回転による突き上げ力との関係を示す変換効率は、平均で2.28(押し載荷時で柱頭ロードセル値が計測できなかった場合(表中の明朝体)を除いて計算)となった。 耐力壁の高さと幅の比は2.90であるので、約2割は耐力壁以外の部分が負担しているか、柱頭ロードセル測定値が低めに計測されている(柱頭ロードセル荷重測定器具の接触不良)などの原因が考えられる。 前述のモデル化によるカウンターウェイト値と上記の変換効率から、推定水平耐力を求めたものを表10にしめす。 その結果、モデル1で約1〜3割程度、モデル2で約3〜5割安全側に水平耐力が算定される結果となった。 |
||||||||||||||||
 |
||||||||||||||||
| 表10:カウンターウェイト値と水平耐力 | ||||||||||||||||
| 4−2−3 押さえ込み係数βによるカウンターウェイト | ||||||||||||||||
| 「3階建て木造住宅の構造設計と防火設計の手引き」(日本住宅・木材技術センター)によると、地震時の耐力壁の剛体的回転による柱の浮き上がりに対する柱脚金物の設計の際、長期軸力以外に上階から何らかの押さえ込み効果があるとして過去の実大実験より得られたβという係数を用いてカウンターウェイトが考慮されている。 | ||||||||||||||||
| それによると、必要柱脚緊結力Rは | ||||||||||||||||
| R=(Q×H/L)×β−V | ||||||||||||||||
| Q:耐力壁に作用する水平力(1/120rad時) H:耐力壁高さ L:耐力壁幅 V:柱の長期鉛直荷重 β:押さえ込み効果係数(耐力壁線端部:0.8、中央部:0.5) |
||||||||||||||||
| で表され、したがって、カウンターウェイトは係数により低減された分と長期鉛直荷重の和 | ||||||||||||||||
| CW=(Q×H/L)×(1−β)+V | ||||||||||||||||
| で表されると考えられる。 | ||||||||||||||||
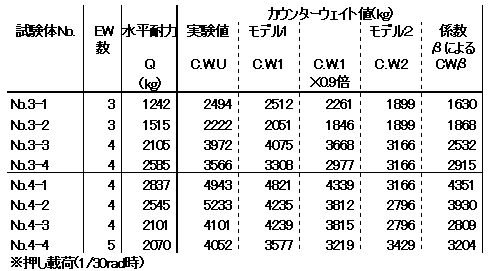
| この計算法によるカウンターウェイト値(今回はQは終局耐力時(層間変形角1/30rad時とする)の水平耐力を耐力壁数で除したものを代入した)を、今回の実験によるカウンターウェイト値CWU、モデル化によるCW1、CW2と共に、表10に示す。 またそれを各試験体の合計値をまとめたものを次ページに簡単な表に示す。 |
||||||||||||||||
| 下表を見ると全体的に今回のモデル化による値より若干小さめの値となったが、直交壁に金物抵抗がある場合のNo.3-2、No.3-4、No.4-4において、ほぼ今回のモデル化と同様の値となった。 梁と柱が金物等によりある程度固められている建物においては、全体的に見た場合にはβによって適当なカウンターウェイトが考慮されていることがいえる。 しかしながら、別表中の各梁ごとのカウンターウェイト値を比較(CWU/CWβが1以下で危険側)すると、多少危険側にカウンターウェイトが算出されている場合があることがわかる(No.3-4、4-1のX9通りの梁で、約2割程度危険側となっている)。 現在の3階建て木造建物の設計に使用されているβという係数では、ある程度カウンターウェイトは考慮できているものの、場合によってはやや過大に評価されることがあるのではないかと思われる。 |
||||||||||||||||
 |
||||||||||||||||
| 表9 | ||||||||||||||||
| ●<たはら・まさる> 構造設計家 「木構造建築研究所 田原」主宰 http://www4.kcn.ne.jp/~taharakn 大阪工業大学大学院 建築学科 客員教授 月刊杉web単行本『杉という木材の建築構造への技術活用』 http://www.m-sugi.com/books/books_tahara.htm |
||||||||||||||||
Copyright(C)
2005 GEKKAN SUGI all rights reserved |
|||